Question

The dimensions of a rectangle are x+3 and x+4. The area of the rectangle is 72. Set up an equation that models this rectangle and solve in order to determine the value of x.

Answer 1

Answer: x = 5

Explanation:

The area of a rectangle is the length times the width. Since the dimensions are given as functions of x, youre going to have to use FOIL to combine them, then set that answer equal to the given value of 72.

l*w = (x+3)*(x+4) = x^2 + 7x +12 = 72

Subtract 72 on both sides. There is a reason why we'll do this instead of subtracting 12. The quadratic formula will help us to solve for x.

x^2 + 7x - 60 = 0

Apply the quadratic formula

`(-7 (+/-)√(7^2-(4)*(1)*(-60) )/(2*1) =(-7(+/-)17)/(2)`

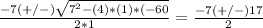
We cant have a negative x value because that would result in negative dimensions and a negative area, which is impossible in this context. So you want to add the 17 instead of subtracting it.

x = 5 and x = -12

An alternate way is just factoring the trinomial to:

(x+12)(x-5) = 0