Question

Put the equation in standard form

Answer 1

`\left(x - {\left\bold{[4\right]}}\right)^2 + \left(y - \left\bold{[10\right]}\right)^2 =\left[\bold{1}\right]`

Explanation:

The given equation
`x^2+y^2-8x-20y+115=0\quad\quad(1)`

is the equation of a circle

The standard form of the equation for a circle is

`(x - a)^2 + (y-b)^2 = r^2\\\\where\\\\center\;of\;circle = (a, b)\\\\r = radius`

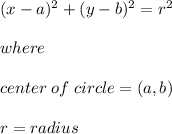
To convert equation (1) to standard form

• Move the constant to the right side:
  
  `x^2+y^2-8x-20y = -115`
  
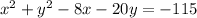
• Group x and y variables:
  
  `\left(x^2-8x\right)+\left(y^2-20y\right)=-115`
  
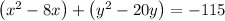
• Convert (x²- 8x) to square form by adding 16 on both sides
  
  `\left(x^2-8x+16\right)+\left(y^2-20y\right)=-115+16`
  
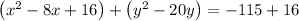
• Convert (y² - 20y) to square form by adding 100 to both sides:
  
  `\left(x^2-8x+16\right) + \left(y^2-20y+100\right) = -115 + 16 + 100\\\\`
  
• 
  `\left(x^2-8x+16\right) = (x-4)^2`
  
  `\left(y^2-20y+100\right) =(y - 10)^2`

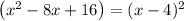
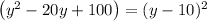
Therefore we get

`\left(x-4\right)^2+\left(y-10\right)^2=-115+16+100\\\\\implies \left(x-4\right)^2+\left(y-10\right)^2= 1`

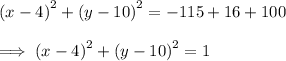
1 = 1²

So the standard form is

`\left(x-4\right)^2+\left(y-10\right)^2=-115+16+100\\\\\implies \boxed{\left(x-4\right)^2+\left(y-10\right)^2= 1^2}`

This indicates a circle with center (4, 10) with radius r = 1