Question

Suppose that 3\%3%3, percent of over 200{,}000200,000200, comma, 000 books borrowed from a library in a year are downloaded. The librarians plan to take an SRS of 757575 books from the population of borrowed books to see what proportion of books sampled are downloaded. What are the mean and standard deviation of the sampling distribution of the proportion of downloaded books

Answer 1

The mean of the sampling distribution of the proportion of downloaded books is 0.03 and the standard deviation is 0.0197.

Explanation:

Central Limit Theorem

For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean
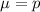`\mu = p` and standard deviation
`s = \sqrt{(p(1-p))/(n)}`

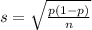
3% of books borrowed from a library in a year are downloaded.

This means that
`p = 0.03`

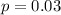
SRS of 75 books.

This means that
`n = 75`

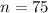
What are the mean and standard deviation of the sampling distribution of the proportion of downloaded books

By the Central Limit Theorem

Mean:
`\mu = p = 0.03`

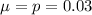
Standard deviation:
`s = \sqrt{(p(1-p))/(n)} = \sqrt{(0.03*0.97)/(75)} = 0.0197`

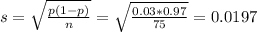
The mean of the sampling distribution of the proportion of downloaded books is 0.03 and the standard deviation is 0.0197.