Answer:
-2.7333 cm/s
Explanation:
As a result of the straightforward harmonic motion, which is represented by the equation s(t) = 3 sin t, where s is measured in centimeters and t in seconds.
The rate of oscillation
The rate of change of s(t) with respect to time determines how quickly the spring oscillates.

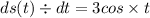
t = 9 s
We now change t = 9 into ds(t)/dt to determine the spring's oscillation rate at t = 9.
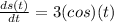

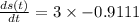
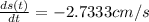
What is simple harmonic motion?
If the restoring force acting on a particle is (1) always oriented toward its mean position and (2) proportionate to its deviation from the mean position, the particle is said to be in simple harmonic motion.
Consider a particle travelling at a constant angular speed w around a circle of radius A. (omega). Let the circle's two diameters along the X- and Y-axes be XOX' and YOY', respectively. Let the circulating particle be at the very right end of the horizontal diameter at time t = 0. Let the particle to circle in a counterclockwise direction. Imagine perpendiculars being drawn on the horizontal diameter starting from the particle's location on the circle. The foot of the perpendicular from its place on the circle to the horizontal diameter performs a straightforward harmonic motion while the particle rotates with constant angular speed. The foot of the perpendicular moves back and forth in a SHM. The simple harmonic motion's time period is equal to how long it takes the particle to complete one circumferential rotation. The time period of SHM is T = 2/w since the particle's angular speed is w.
SHM is hence cyclical. But so also is the particle's rotational movement around the circle. Yet, the particle's motion is not simple harmonic. The perpendicular's foot is being subjected to SHM.
Hence, not every periodic motion is simple harmonic, but all simple harmonic motion is periodic.
Thanks.