Question

Please help!! solve for x

Answer 1

x = 1/4, 3/4

Explanation:

From
`\displaystyle{x+x^2+\dots + x^n + \dots}` can be rewritten as:

`\displaystyle{(x)/(1-x)}`

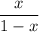
through the infinite geometric series formula for |x| < 1 which is:

`\displaystyle{S = (a_1)/(1-r)}`

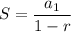
In the series,
`\displaystyle{a_1}` is our first term which is x and r is common ratio which is also x (by dividing next term by previous term. Hence, x²/x = x). Thus, we have the following rewritten equation:

`\displaystyle{-1+(1)/(x)+(x)/(1-x) = (10)/(3)}`

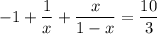
Solve the equation for x:

`\displaystyle{-1 \cdot 3x(1-x)+(1)/(x) \cdot 3x(1-x)+(x)/(1-x)\cdot 3x(1-x) = (10)/(3) \cdot 3x(1-x)}\\\\\displaystyle{-3x(1-x)+3(1-x)+3x^2=10x(1-x)}\\\\\displaystyle{-3x+3x^2+3-3x+3x^2=10x-10x^2}\\\\\displaystyle{3x^2+3x^2+10x^2-3x-3x-10x+3=0}\\\\\displaystyle{16x^2-16x+3=0}\\\\\displaystyle{\left(4x-1\right)\left(4x-3\right)=0}\\\\\displaystyle{x=(1)/(4), (3)/(4)}`

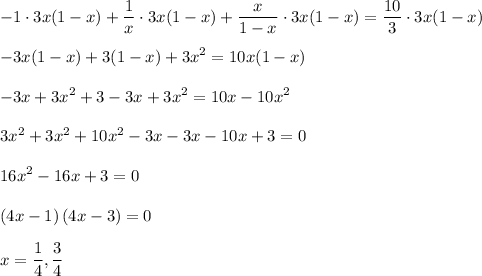
Both solutions work since 1/4 and 3/4 are less than 1.