Question

Prime to determine the HCF and LCM of 84 and462
​

Answer 1

Given: Find the HCF & LCM of 84 and 462.

First, to find the HCF, solution by factorization:

The factors of 84 are: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84.

The factors of 462 are: 1, 2, 3, 6, 7, 11, 14, 21, 22, 33, 42, 66, 77, 154, 231, 462.

Then the greatest common factor is 42.

Then, to find the LCM, solution by prime factorization:

List all prime factors for each number.

Prime Factorization of 82 is:

2 x 41 =>
`2^1 x 41^1`

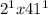
Prime Factorization of 462 is:

2 x 3 x 7 x 11 =>
`2^1 x 3^1 x 7^1 x 11^1`

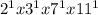
For each prime factor, find where it occurs most often as a factor and write it that many times in a new list.

The new superset list is

2, 3, 7, 11, 41

Multiply these factors together to find the LCM.

LCM = 2 x 3 x 7 x 11 x 41 = 18942

In exponential form:

LCM =
`2^1 x 3^1 x 7^1 x 11^1 x 41^1 = 18942`

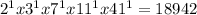
LCM = 18942

Therefore,

LCM(82, 462) = 18,942

Have a wonderful day! :-)