Question

I need someone to explain how this is done

2x^3-16=0

Answer 1

The solution to the given cubic equation is x = 2.

Explanation:

To solve the cubic equation 2x³ - 16 = 0, use algebraic operations to isolate x.

Add 16 to both sides of the equation:

`\implies 2x^3-16+16=0+16`

`\implies 2x^3=16`

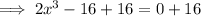
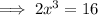
Divide both sides of the equation by 2:

`\implies (2x^3)/(2)=(16)/(2)`

`\implies x^3=8`

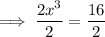
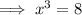
Rewrite 8 as 2³ since 2 × 2 × 2 = 8:

`\implies x^3=2^3`

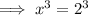
Take the cube root of both sides of the equation:

`\implies \sqrt[3]{x^3}=\sqrt[3]{2^3}`

`\implies x=2`

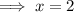
Therefore, the solution to the given cubic equation is x = 2.