Question

Find the value of x. round to the nearest tenth, use law of cosines

Answer 1

x = 118.6°

Explanation:

Law Of Cosines

In trigonometry, the law of cosines (also known as the cosine formula, cosine rule) relates the lengths of the sides of a triangle to the cosine of one of its angles.

If a, b and c are three sides of a triangle and θ is the included angle of the sides a and b then the cosine rule states:

`c^2 = a^2 + b^2 - 2ab\cos \theta`

In this diagram we are asked to find angle x

The sides that include angle x are AB and BC

The third side is AC

We have

`AB = 23\\BC = 20\\AC = 37\\`

`m\angle ABC = x^\circ`

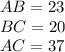
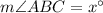
Therefore by the law of cosines,

AC² = AB² + BC² - 2(AB)(AC) cos(x)

⇒ 37² = 23² + 20² - 2(23)(20) cos(x)

⇒ 1369 = 529 + 400 - 920 cos(x)

Move -920cos(x) from right to left side(sign changes)
920cos(x) + 1369 = 929

Move 1369 to right side (sign changes)
920cos(x) = - 1369 + 929
= -440

Divide both sides by 920:

`cos(x) = - (440)/(920) \\\\x = cos^(-1) \left(- (440)/(920)\right)`

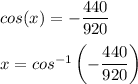
Using a calculator this works out to
x = 118.6° rounded to the nearest tenth