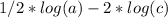Question

I need help please, I’ll give extra points for right answers

Answer 1

Answer and Explanation:

To solve these four problems, we need to make use of three rules of logs, namely the product rule, the quotient rule, and the power rule.

(a) The product rule says that the log of a product of two terms (or arguments) is equivalent to the sum of the logs of each term individually:

`log(ab)=log(a)+log(b)`

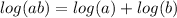
(b) The quotient rule says that the log of a quotient of two terms is equivalent to the difference of the logs of each term individually:

`log((a)/(b))=log(a)-log(b)`

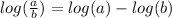
(c) The power rules says that if the term inside a log has an exponent, then the exponent can be moved to the front of the log for multiplication:

`log(a^b)=b*log(a)`

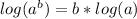
(1) For this first problem, we see that a^2 and c are multiplied together so we can first rewrite them as sums of the single logs:

`log(a^2c)\\log(a^2)+log(c)`

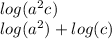
Now we can bring the "2" down in the first log:

`2*log(a)+log(c)`

(2) The rules of logs also apply to natural logs (i.e., ln) so our process doesn't change. Thus, we still rewrite the log as the difference of single natural logs:

`ln((a)/(b))\\ ln(a)-ln(b)`

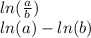
(3) We can first rewrite the log as the difference of the single logs:

`log((c^3)/(b))\\\\ log(c^3)-log(b)`

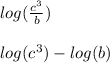
Now, we can bring the "3" down in the first log:

`3*log(c)-log(b)`

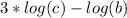
(4) We can first rewrite the log as the difference of single logs:

`log(√(a) )/(c^2)\\ \\log(√(a))-log(c^2)`

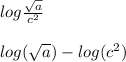
We must remember that taking the square root of a number is the same as raising that number to 1/2 or 0.5. Thus, the equation we now have is

`log(a^1^/^2)-log(c^2)`

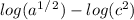
Now, we can bring the "1/2" in front of its log and the "2" in front of its log

`1/2*log(a)-2*log(c)`