Question

What is L'Hôpital's rule in differentiation?

Answer 1

Problem Statement

The question asks us what L'Hopital's rule in differentiation is.

Solution

What is L'Hopital's rule?

L'Hopital's rule is the rule used when we are given a limit of a function to evaluate and then, we differentiate the numerator and denominator of the function before applying the limits to the function.

When is L'Hopital's rule used?

The L'Hopital's rule is used whenever directly solving the limit of a function leads to an indeterminate value like:

`(0)/(0)\text{ or }(\infty)/(\infty)`

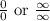
For example, if we have the following limit of a function:

`\lim _(x\to\infty)(x^2)/(e^x)`

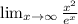
Direct substitution of the limit of positive infinity into the function yields:

`\begin{gathered} (\infty^2)/(e^(\infty)) \\ By\text{ the rules of infinity:} \\ \infty^2=\infty \\ e^(\infty)=\infty \\ \\ \therefore(\infty^2)/(e^(\infty))=(\infty)/(\infty) \end{gathered}`

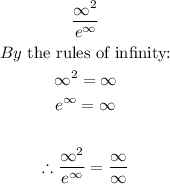
This result is indeterminate.

Thus, we should apply L'Hopital's rule.

Applying L'Hopital's rule to this example, we have:

`\begin{gathered} \text{Differentiating the numerator:} \\ \frac{\mathrm{d}x^2}{dx}=2x \\ \\ \text{Differentiating the denominator:} \\ (de^x)/(dx)=e^x \\ \\ \therefore\lim _(x\to\infty)(x^2)/(e^x)\to\lim _(x\to\infty)(2x)/(e^x) \\ \text{Applying the limit, we have:} \\ =(2*\infty)/(e^(\infty))=(\infty)/(\infty) \end{gathered}`

The result is still indeterminate. Thus, we apply L'Hopital's rule once more.

`\begin{gathered} \text{Differentiate the new numerator:} \\ (d(2x))/(dx)=2 \\ \\ \text{Differentiating the denominator:} \\ (d(e^x))/(dx)=e^x \\ \\ \text{Thus, we have:} \\ \lim _(x\to\infty)(x^2)/(e^x)\to\lim _(x\to\infty)(2)/(e^x) \\ \\ \text{Applying the limit, we have:} \\ =(2)/(e^(\infty))=(2)/(\infty)=0 \end{gathered}`

Thus, the limit of the function given as x tends to infinity is ZERO (0)