Question

14. In the diagram below, DE is parallel to AB. Solve for x.

Answer 1

`\large\boxed{ \sf x = 5.35 }`

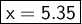
Explanation:

We need to find out the value of "x" in the given figure. Here we are given that DE is parallel to AB , so here we can make use of Thale's Theorem :-

Thale's Theorem:-

If a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio .

Here line DE divides two sides AC and BC .

Now by Thale's Theorem, we have;

`\sf:\implies (CD)/(AD)=(CE)/(BE) \\`

Substitute the the respective values,

`\sf:\implies (16)/(8)=(10.7)/(x) \\`

`\sf:\implies x =(8(10.7))/(16)\\`

`\sf:\implies\pink{ x = 5.35 } \\`

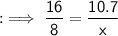
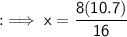
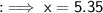
Hence the value of x is 5.35 .

Answer 2

The value of x is 5.4 units (nearest tenth).

Explanation:

The Side Splitter Theorem states that if a line parallel to one side of a triangle intersects the other two sides, then this line divides those two sides proportionally.

As DE is parallel to AB, we can calculate the value of x by using the Side Splitter Theorem.

Therefore:

`\implies \sf AD : DC = BE : EC`

`\implies 8: 16= x : 10.7`

`\implies (8)/(16)=(x)/(10.7)`

Multiply both sides of the equation by 10.7:

`\implies (8)/(16) \cdot 10.7=(x)/(10.7) \cdot 10.7`

`\implies 0.5 \cdot 10.7=x`

`\implies x=5.35`

Therefore, the value of x is 5.4 units rounded to the nearest tenth.