Question

8. Solve for x. Round your answer to the nearest tenth if necessary.

Answer 1

Equate the triangle through their angles and see whether they are similar

• 180-(61+52)
• 180-113
• 67°

2nd

• 180-67+61
• 52°

Triangles are equal

the sides must be proportional

• x/39=16/19
• 19x=16(39)
• x=32.8 units

Answer 2

The length of line segment PR is 32.8 units to the nearest tenth.

Explanation:

Interior angles of a triangle sum to 180°.

Therefore, the measure of angle O in triangle MNO can be calculated as follows:

`\implies m \angle M + m \angle N + m \angle O=180^(\circ)`

`\implies 61^(\circ) + 52^(\circ) + m \angle O=180^(\circ)`

`\implies 113^(\circ) + m \angle O=180^(\circ)`

`\implies m \angle O=67^(\circ)`

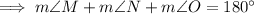
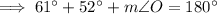
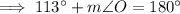
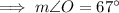
Therefore, the three angles in triangle MNO are:

• m∠M = 61°
• m∠N = 52°
• m∠O = 67°

As two angles in triangle PQR are the same as two of the angles in triangle MNO, the three angles are the same in both triangles.

• m∠M = m∠P = 61°
• m∠N = m∠Q = 52°
• m∠O = m∠R = 67°

Therefore, triangle MNO is similar to triangle PQR.

As corresponding sides are always in the same ratio in similar triangles:

`\implies \sf MN:PQ=NO:QR=MO:PR`

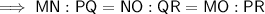
From inspection of the given triangles:

• MN = 19
• MO = 16
• PQ = 39
• PR = x

Substitute these values into the relevant ratio:

`\implies \sf MN:PQ=MO:PR`

`\implies 19:39=16:x`

`\implies (19)/(39)=(16)/(x)`

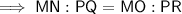
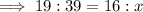
Cross multiply:

`\implies 19 \cdot x=16 \cdot 39`

`\implies 19x=624`

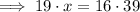
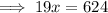
To solve for x, divide both sides by 19:

`\implies (19x)/(19)=(624)/(19)`

`\implies x=32.8421052...`

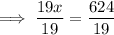
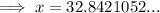
Therefore, the length of line segment PR is 32.8 units to the nearest tenth.