Question

5. Triangle MNO is similar to triangle PQR. What is the measure of side QR?

Answer 1

13qr/13•400/13

Qr= 30.8

The value of Qr is approximately 30.8

Answer 2

The length of line segment QR is 30.8 units (nearest tenth).

Explanation:

In similar triangles, corresponding sides are always in the same ratio.

Therefore, if triangle MNO is similar to triangle PQR then:

`\implies \sf MN:PQ=NO:QR=MO:PR`

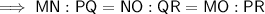
From inspection of the given triangles, the measures of the side lengths are:

• MN = 13
• NO = 10
• PQ = 40

Substitute these values into the relevant ratio to create an equation:

`\implies \sf MN:PQ=NO:QR`

`\implies \sf 13:40=10:QR`

`\implies \sf (13)/(40)=(10)/(QR)`

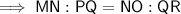
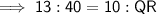
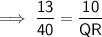
Cross multiply:

`\implies \sf 13 \cdot QR=10 \cdot 40`

`\implies \sf 13 \:QR=400`

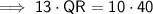
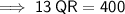
Divide both sides by 13:

`\implies \sf (13 \:QR)/(13)=(400)/(13)`

`\implies \sf QR=30.7692307...`

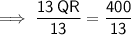
Therefore, the length of line segment QR is 30.8 units to the nearest tenth.