Question

Hi, can you help me answer this question please, thank you!

Answer 1

a) test statistic = 1.280

b) p-value = 0.1003

c) greater than alpha

d) reject the null

e) There is sufficient evidence to warrant rejection of the claim that the population mean is not equal to 70.5

Explanation:

The test statistic for this given sample is as follows:

`\begin{gathered} z=\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt[]{n}}} \\ \text{ replacing:} \\ z=\frac{72.7-70.5}{\frac{11.4}{\sqrt[]{44}}} \\ z=1.280 \end{gathered}`

The p-value, we calculate it thanks to the following table:

Therefore:

`\begin{gathered} p(z<1.28)=p(z<-1.28)=0.1003 \\ \text{ p-value = 0.1003} \end{gathered}`

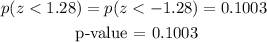
The result is not significant at alpha < 0.05.

c) The value of alpha is 0.05 and that of p is 0.1003, therefore the value of pe is greater than the value of alpha

d) When alpha is 0.05, the critical value is ± 1.96.

Hence, z is equal a 1.28, the test statistic is in the critical value.

The decision rule is reject the null hypothesis

e) The final conclusion would be there is enough sample evidence to support the claim that the population is mean is not equal to 70.5