Answer:
M.A = 8
Step-by-step explanation:
Given the following data;
Circumference = 2cm
Number of threads = 4
To find the mechanical advantage (M.A);
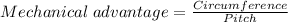
But,
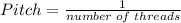
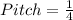
Pitch = 0.25
Substituting the values into the equation, we have;
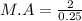
M.A = 8
Therefore, the mechanical advantage of the screw is 8.