Question

B, d, and f are the midpoints of each side and g is the centroid. find the following lengths

please do not give an answer if you cannot help.​

Answer 1

see explanation

Explanation:

AD , BE and CF are medians of the triangle.

On each median the distance from the vertex to the centroid is twice as long as the distance from the centroid to the midpoint.

(1)

given BG = 5

GE = 2 × BG = 2 × 5 = 10

BE = BG + GE = 5 + 10 = 15

(2)

given CG = 16

GF =
`(1)/(2)` × CG =
`(1)/(2)` × 16 = 8

CF = CG + GF = 16 + 8 = 24

(3)

given AD = 30

AG =
`(2)/(3)` × AD =
`(2)/(3)` × 30 = 2 × 10 = 20

GD =
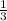`(1)/(3)` × AD =
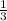`(1)/(3)` × 30 = 10

(4)

given GF = x

GC = 2 × GF = 2 × x = 2x

CF = CG + GF = x + 2x = 3x

(5)

given AG = 9x , GD = 5x - 1

AG = 2 GD , that is

9x = 2(5x - 1)

9x = 10x - 2 ( subtract 9x from both sides )

0 = x - 2 ( add 2 to both sides )

2 = x

then

AD = AG + GD

= 9x + 5x - 1

= 14x - 1 ( substitute x = 2 )

= 14(2) - 1

= 28 - 1

= 27