Question

Please, Help me with this question

Answer 1

The quadratic equation
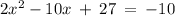`2x^2-10x\:+\:27\:=\:-10` has no real roots

The two complex roots are:

`x = 2.5 + 3.5 \, i\\\\and\\\\x = 2.5 - 3.5 \, i`

Explanation:

There are no real root solutions to this quadratic equation

The quadratic formula for solving an equation of the standard form

`ax^2 + bx + c = 0`

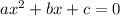
is given by

`x = ( -b \pm √(b^2 - 4ac))/( 2a )`

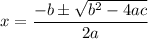
The term under the square root is called the discriminant and determines the type number of roots(solutions) to the quadratic

• When
  `b^2 - 4ac=0` there is one real root.
• When
  `b^2 - 4ac > 0` there are two real roots.
• When
  `b^2 - 4ac < 0` there are no real roots - roots are complex

The given quadratic equation is

`2x^2-10x\:+\:27\:=\:-10`

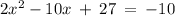
Add 10 to both sides:

`2x^2-10x\:+\:37\:=0`

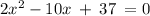
Comparing to the standard form we see
a = 2, b = -10, c = 37

The discriminant is

`b^2 - 4ac = (-10)^2 - 4\cdot2\cdot 37\\= 100 - 296\\= -196`

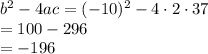
Since the discriminant is negative both roots will be comples

`x = ( -b \pm √(b^2 - 4ac))/( 2a )\\\\x = ( -(-10) \pm √((-10)^2 - 4(2)(37)))/( 2(2) )\\\\x = ( 10 \pm √(100 - 296))/( 4 )\\\\x = ( 10 \pm √(-196))/( 4 )`

`\text {To find $√(-196)$}`

`√(-196) = √(196)√(-1) =√(196)\;i`

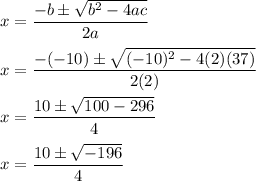
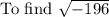
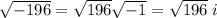
where i =
`√(-1)`

We have


`√(196) = 14\\\\So\\\\√(-196) = 14i`

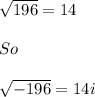
The solutions are

`x = ( 10 \pm 14\, i)/( 4 )`

`x = ( 10 )/( 4 ) \pm (14\, i)/( 4 )`

`x = ( 5)/( 2 ) \pm ( 7\, i)/( 2 )`

`x = 2.5 \pm 3.5i`

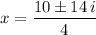
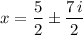
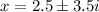
The two complex solutions are:

`x = 2.5 + 3.5 \, i\\\\and\\\\x = 2.5 - 3.5 \, i`