Question

In many cases, removing dangerous chemicals from waste sites can be modeled using exponential decay. This is a key reason why such cleanups can be dramatically expensive. Suppose for a certain site there are initially 20 parts per million of a dangerous contaminant and that our cleaning process removes 5% of the remaining contaminant each day. How much contaminant (in parts per million) is removed during the first three days? Round your answer to two decimal places

Answer 1

Recall that the exponential decay is given by

`P=P_0(1-r)^t`

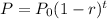
Where

P = Amount of contaminant after time t

P₀ = Initial amount of contaminant = 20 ppm

r = rate of decay = 5% = 0.05

t = time in days = 3

Substitute the given values into the above equation

`\begin{gathered} P=20(1-0.05)^3 \\ P=20(0.95)^3 \\ P=17.15 \end{gathered}`

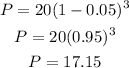
This means that 17.15 ppm will be left after the first 3 days.

20 - 17.15 = 2.85 ppm

Therefore, 2.85 ppm is removed during the first three days.