Question

Find the length of X

Answer 1

Similar Triangles

Similar triangles have different dimensions, but their measurements have the same ratio.

Solving the Question

In the image, we can see two triangles. A large triangle and a small triangle. These are similar. How can we tell? They share the same angles.

Now, we can set up a proportion comparing their side lengths:

`(82)/(28)=((2x+8)+(5x-4))/(2x+8)`

Theoretically, if we divide corresponding side lengths of two similar shapes, we should get the same value. This is what makes the proportion true.

Now, simplify:

`(82)/(28)=((2x+8)+(5x-4))/(2x+8)`

• First, simplify the fraction on the left:

`(41)/(14)=((2x+8)+(5x-4))/(2x+8)`

• Remove the fractions by multiplying each side by the denominators:

`41(2x+8)=14[(2x+8)+(5x-4)]`

• Expand the parentheses:

`82x+328=14[2x+8+5x-4]\\82x+328=14(7x+4)\\82x+328=98x+56`

• Combine like terms:

`328=16x+56\\272=16x\\x=17`

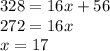
Answer

x = 17