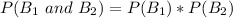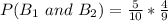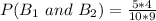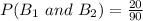Question

10 marbles what is the probability of drawing 2 blue marbles if the first marble is placed back in the bag before the second draw

Answer 1

Complete Question:

There are 10 marbles. What is the probability of drawing 2 blue marbles if the first marble is NOT placed back in the bag before the second draw.

2 yellow, 3 pink, 5 blue

Answer:

`P(B_1\ and\ B_2) = (2)/(9)`

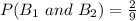
Explanation:

Given

`Blue = 5`

`Pink = 3`

`Yellow = 2`

`Total = 10`

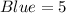
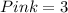
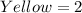
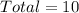
When the first blue marble is selected, the probability is:

`P(B_1) = (n(Blue))/(Total)`

`P(B_1) = (5)/(10)`

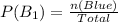
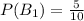
Since the first marble is not returned, we have the following marbles left

`Blue = 4`

`Pink = 3`

`Yellow = 2`

`Total = 9`

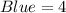
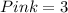
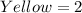
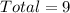
The probability of picking a second blue marble is:

`P(B_2) = (n(Blue))/(Total)`

`P(B_1) = (4)/(9)`

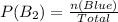
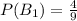
So, the required probability is:

`P(B_1\ and\ B_2) = P(B_1) * P(B_2)`

`P(B_1\ and\ B_2) = (5)/(10) * (4)/(9)`

`P(B_1\ and\ B_2) = (5*4)/(10*9)`

`P(B_1\ and\ B_2) = (20)/(90)`

`P(B_1\ and\ B_2) = (2)/(9)`