Question

Sienna Rose received $3500 cash in graduation presents. She invests it in an account earning 3.35% interest compounded monthly. How long will it take for her money to grow to $5500 ?

Answer 1

It will take about 13.5 years for the money to grow to $5,500
That would be about 13 years and 6 months

Explanation:

The formula for accrued amount(principal + interest) is given by:

`A = P\left(1 + (r)/(n)\right)^(nt)\quad(1)\\`

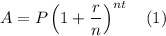
where
P = Principal amount
r = R/100 where R is the annual interest rate as a percentage
n= number of times compounded per year
t = number of years

Given

A = $5,600
P = $3,500
R = 3.35% ==> r = 3.35/100 = 0.0335
n = 12 (since there are 12 months in a year)

We have to find out t

Plugging known values into equation (1)

`5500 = 3500\left(1+ (0.0335)/(12)\right)^(12t)\\\\5500 = 3500 \left(1+ 0.002791\right)^(12t)\\\\5500 = 3500 (1.002791)^(12t)`

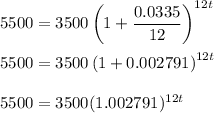
Switch sides so unknown appears on the left side:

`3500 (1.002791)^(12t) = 5500`

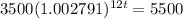
Divide by 3500 both sides:

`(1.002791)^(12t) = (5500 )/(3500)\\\\(1.002791)^(12t) = 1.5714\\\\`

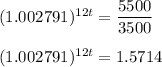
Take logs on both sides:

`\ln \left(1.002791^(12t)\right)=\ln \left(1.5714\right)\\\\`

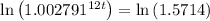
We have

`\ln \left(1.002791^(12t)\right) = 12t\ln \left(1.002791\right)\\\\`

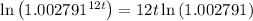
Therefore we get

`12t\ln \left(1.002791\right)=\ln \left(1.5714\right)\\\\t\ln \left(1.002791\right)=\ln \left(1.5714\right)\\\\\\`

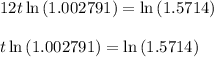
Dividing both sides by
`12\ln \left(1.002791\right)` this works out to

`t=(\ln \left(1.5714\right))/(12\ln \left(1.002791\right))`

`t = 13.51359\; years`

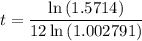
Rounding to one decimal place

`t = 13.51\; years\\`

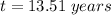
This would be roughly 13 years and 6 months