Answer:
Explanation:
You want to know when Roxanne and Maya will have read the same number of pages, and how many pages they will have read, if Roxanne has read 93 pages and reads 2 pages per minute, while Maya has read 15 pages and reads 4 pages per minute.
Fractions
You know that multiplying a fraction by its denominator cancels the denominator and leaves the numerator:
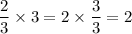
The same is true when variables or units are involved:
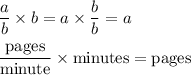
Rates
The word "per" in a math context usually means "divided by". In a grocery store, you might see a unit rate tag with units of "cents per ounce". Expressed as a fraction, that is ...
cents/ounce
Multiplying this value by the number of ounces will tell you the cost in cents.
A rate of "pages per minute" expresses a rate with the units of pages divided by minutes. When you multiply that rate by minutes, you get pages, as shown above. Recognizing this can help you write the equation for the number of pages each girl reads.
Units and amounts
It is well known that "you cannot add apples and oranges." Similarly, you cannot add quantities that have different units. It make no sense to add seconds and pounds, for example. So, when writing equations, considering the units involved can help get things right.
For this problem, we want the numbers of pages read by each friend to be the same number. For each friend the number of pages read is ...
total pages read = (initial number read) + (pages per minute) × minutes
You will notice the unit of each of the terms is pages. Since the units are the same, we know we can add the terms without difficulty.
Roxanne
Roxanne is described as having read 93 pages, and reading additional pages at the rate of 2 per minute. Her number of pages read will be ...
Roxanne's pages read = 93 +2m . . . . . . . m is the number of minutes
Maya
Maya is described as having read 15 pages, and reading additional pages at the rate of 4 per minute. Her number of pages read will be ...
Maya's pages read = 15 +4m . . . . . . . . . . . m is the number of minutes
Equal pages
The numbers of pages read will be the same when ...
Maya's pages = Roxanne's pages
15 +4m = 93 +2m . . . . . . . . substitute the expressions for pages read
2m = 78 . . . . . . . . . . . . subtract 2m+15
m = 39 . . . . . . . . . . . . . (minutes) divide by 2
The numbers of pages each friend will have read after 39 minutes is ...
93 +2m = 93 +78 = 171 . . . . . (pages)
Roxanne and Maya had each read 171 pages after 39 minutes.
Graph
We find solving equations like this to be less work when it is done by a graphing calculator. The point (time, pages) where the lines cross is the point where the friends have read the same total number of pages in the same number of minutes. It is the answer to the question:
(39 minutes, 171 pages)
__
Additional comment
We have tried to help you see that understanding the units of a problem goes a long way toward understanding how the parts of the problem are related to each other. In many math problems, and especially in physics problems, it is useful to keep the units with the number. As you can see, math operations can be performed on units the same as for any variable. If the units don't work out, the chances are good that the math is wrong.