Question

Two systems of equations are given below.

For each system, choose the best description of its solution.
If applicable, give the solution.

Answer 1

A: No solution

B: Unique Solution: (0, 0)

Explanation:

System A:

In System A, you may notice that in both equations the two equations have variables with the same coefficient, and this is ideal for the elimination method of solving the equation. We want to add the equations in a way that cancels out variables. So let's multiply the top equation by negative one:
`-1(2x+3y)=-(9)\implies -2x-3y=-9`

Now from here we want to add the two equations:

`\ \ -2x-3y=9\\+2x+3y=4\\0+0=13`

And the statement provided is clearly not true, 0 is never equal to 13, meaning the systems of equation has no solution, which occurs when you have two parallel lines.

System B:

In this case, we can easily solve this using substitution, since y is equal to 7x that means we can substitute in 7x for y in the second equation:

`y=x\implies 7x=x`

And from here we subtract x from both sides, and divide by 6 giving us:

`x=0`

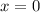
And now we can take this value and plug it into either equation to solve for our y value, and it's most convenient to plug it into the y = x equation... since there's nothing to solve, we just get:

y = 0

So x = 0, and y = 0, meaning there is a unique solution of (0, 0)