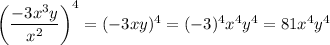Answer:
see attached
Explanation:
No doubt you have examples showing the wording that is expected to be used here. We have made a guess.
power of a ratio: the numerator is raised to the power, as is the denominator. (a/b)^c = (a^c)/(b^c)
power of a product: each factor is raised to the power. (ab)^c = (a^c)(b^c)
power of a power: the powers are multiplied. (a^b)^c = a^(bc)
quotient of powers: the result when one power is divided by another is the difference of the numerator and denominator powers. (a^b)/(a^c) = a^(b-c)
_____
Additional comment
The order of operations tells you to simplify inside parentheses first. Doing that reduces the work somewhat.