Question

Find the zeros and give the multiplicity.
f(x) = x2(5x + 6)9(x − 8)2

Answer 1

Zeroes & Multiplicity:

x = 0 : Multiplicity = 2

x = -6/5 : Multiplicity = 9

x = 8 : Multiplicity = 2

Explanation:

The equation provided is:
`f(x)=x^2(5x+6)^9(x-8)^2`

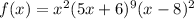
Factored Form:

We're given the polynomial in factored form, which just means the polynomial is broken down into each of its factors. This is a really convenient form to have a polynomial in as we can easily find the zeroes of the polynomial.

This is due to the Zero Property of Multiplication, which essentially states zero times any number results in zero. So we just have to set each factor equal to zero, and solve, since if one of the factors is zero, then the entire thing becomes zero.

So this gives us the following equations:

`x^2=0\implies x = 0\\\\(5x+6)^9=0\implies x = -(6)/(5)\\\\(x-8)^2=0\implies x = 8`

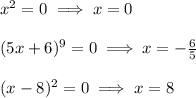
Now for the multiplicity, we just look at the exponent of the factor we set equal to zero. So x^2 gives us a zero of x = 0, and the exponent is 2, which is also the multiplicity of this zero.

The (5x + 6)^9 gives us a zero of x = -6/5, and the exponent is 9, which is also the multiplicity of the zero. Same thing applies for the zero at x = 8, which has a multiplicity of 2.