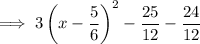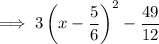Question

Complete the square for 3x^2 - 5x - 2

Answer 1

`3\left(x-(5)/(6)\right)^2-(49)/(12)`

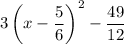
Explanation:

Given quadratic expression:

`3x^2 - 5x - 2`

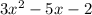
To complete the square, factor out the coefficient of the leading term:

`\implies 3\left(x^2-(5)/(3)x-(2)/(3)\right)`

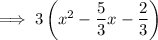
Add and subtract the square of half the coefficient of the term in x inside the parentheses:

`\implies 3\left(x^2-(5)/(3)x+\left(((-5)/(3))/(2)\right)^2-\left(((-5)/(3))/(2)\right)^2-(2)/(3)\right)`

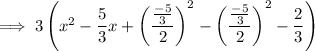
Simplify:

`\implies 3\left(x^2-(5)/(3)x+\left((-5)/(6)\right)^2-\left((-5)/(6)\right)^2-(2)/(3)\right)`

`\implies 3\left(x^2-(5)/(3)x+(25)/(36)-(25)/(36)-(2)/(3)\right)`

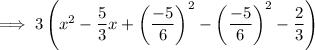
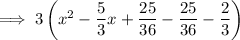
Factor the perfect square trinomial formed by the first three terms inside the parentheses:

`\implies 3\left(\left(x-(5)/(6)\right)^2-(25)/(36)-(2)/(3)\right)`

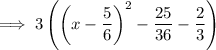
Distribute:

`\implies 3\left(x-(5)/(6)\right)^2-(75)/(36)-(6)/(3)`

`\implies 3\left(x-(5)/(6)\right)^2-(25)/(12)-2`

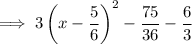
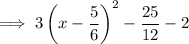
Simplify:

`\implies 3\left(x-(5)/(6)\right)^2-(25)/(12)-(24)/(12)`

`\implies 3\left(x-(5)/(6)\right)^2-(49)/(12)`