Answer:
The probability that the first two chocolates Bob eats will have almonds is 5/51 or 9.8% (nearest tenth).
Explanation:
Given that Bob has a box of chocolates containing 6 chocolate covered almonds, 4 chocolate covered peanuts, and 8 plain chocolates, the total number of chocolates in the box is:

Probability Formula
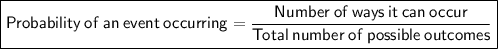
Therefore, the probability that the first chocolate Bob eats will have almonds is:

As Bob has eaten one almond chocolate there are now 5 chocolate covered almonds left and a total of 17 chocolates. Therefore, the probability that the next chocolate Bob eats will have almonds is:

To find the total probability for two or more events, multiply the probabilities. Therefore, the probability that the first two chocolates Bob eats will have almonds is:

Therefore, the probability that the first two chocolates Bob eats will have almonds is 5/51 or 9.8% (nearest tenth).