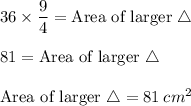Question

The ratio of the sides of two similar is 2/3. The area of the smaller triangle is 36cm. Find the area of the larger triangle?

Answer 1

`\text{Area of larger $\triangle$} = 81 \:cm^2`

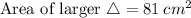
Explanation:

Given.

Ratio of corresponding sides of two similar triangles = 2:3 or
`(2)/(3)`
Area of smaller triangle = 36 cm²

By the property of area of two similar triangle,
Ratio of area of both triangles = (Ratio of their corresponding sides)²

`\frac{\text{Area of smaller $\triangle$ }}{\text{Area of larger $\triangle$ }} = \left((2)/(3)\right)^2}`

`\frac{36}{{\text{Area of larger $\triangle$ }}} = (4)/(9)`

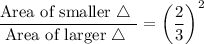
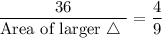
Cross-multiplying we get

`36 * (9)/(4) = \text{Area of larger $\triangle$}\\\\81 = \text{Area of larger $\triangle$}\\\\\text{Area of larger $\triangle$} = 81 \:cm^2`