We are given the following expression:
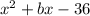
We are asked to determine the value of "b" for which the expression is not factorable.
To factor the expression we take the square root of the first term and we decompose the expression as follows:
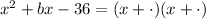
In the blank we need to determine two numbers which product is -36 and their sum is "b". If "b" were 15 we would get:
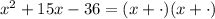
Since there are no numbers that when multiply their product is -34 ans their sum is 15, this value would make the expression not factorable.
In contrast, if we take 16 for example we would get:
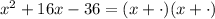
If we take 18 and -2 we get:
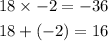
Therefore:
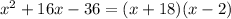
And 16 would make the expression factorable.
Therefore, the answer is 15.