Question

A buoy floats on the surface of the water. The height in meters of the buay t hours after midnight, relative to sea level, is given by the equation f(x)=5cospi/6t+4 Estimate how many hours elapse between the first twotimes the buoy is exactly 6 m above sea level

Answer 1

Given the function:

`f(x)=5cos(\pi)/(6)t+4`

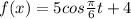
The t is the number of hours after midnight.

Let's estimate how many hours elapse between the first two times the buoy is exactly 6 m above sea level.

We have:

`f(x)=6`

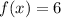
Substitute 6 for f(x) and solve for t.

We have:

`\begin{gathered} 6=5cos(\pi)/(6)t+4 \\ \\ 6-4=5cos(\pi)/(6)t+4-4 \\ \\ 2=5cos(\pi)/(6)t \end{gathered}`

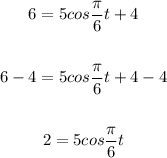
Divide both sides by 5:

`\begin{gathered} (2)/(5)=(5cos(\pi)/(6)t)/(5) \\ \\ (2)/(5)=cos(\pi)/(6)t \end{gathered}`

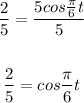
Take the cos inverse of both sides:

`\begin{gathered} cos^(-1)((2)/(5))=(\pi)/(6)t \\ \\ 66.422=(\pi)/(6)t_1 \\ \\ (\pi)/(6)t_1=66.42 \end{gathered}`

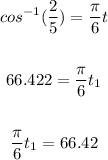
Also, the second angle is:

`\begin{gathered} (\pi)/(6)t=360-66.42 \\ \\ (\pi)/(6)t_2=293.58 \end{gathered}`

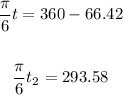
Now, let's solve both equations for t:

`\begin{gathered} t_1=66.42*(6)/(\pi)=(66.42*6)/(180)=2.214 \\ \\ t_2=(293.58*6)/(180)=9.786 \end{gathered}`

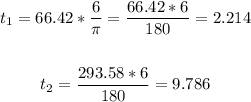
First time = 2.214 hours

Second time = 9.786 hours

Now, to solve for the time, t, we have:

t = t2 - t1 = 9.786 - 2.214 = 7.575 ≈ 7.6 hours.

Therefore, 7.6 hours elapsed between the first two times the buoy is 6m above sea level.

ANSWER:

D. 7.6 hours.