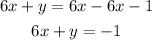Answer:
6x + y = -1
Step-by-step explanation:
The general slope-intercept form of the equation of a line is given as;
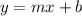
where m = slope of the line
b = y-intercept
Given the below equation of a line;
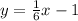
we can see that the slope of the line, m = 1/6 and the y-intercept, b = -1
Any line that will be perpendicular to the above line must have a negative reciprocal of its slope. So if the slope of the given line is 1/6, then the slope of the perpendicular line will be;
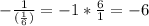
So the slope of the perpendicular is -6, the equation of the line can then be written as;
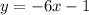
Looking at the given options in the question, we'll need to rewrite the above equation;
Let's add 6x to both sides of the equation, we'll have;