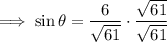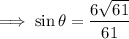Question

I can’t get this right!!!!

Answer 1

`\csc \theta=(√(61))/(6)`

`\sin \theta=(6)/(√(61))=(6√(61))/(61)`

`\cot \theta=(5)/(6)`

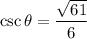
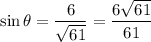
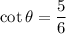
Explanation:

Use Pythagoras Theorem to calculate the length of the hypotenuse of the given right triangle:

`\implies a^2+b^2=c^2`

`\implies 5^2+6^2=c^2`

`\implies 25+36=c^2`

`\implies c^2=61`

`\implies c=√(61)`

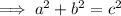
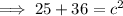
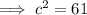
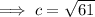
Therefore:

• The side opposite angle θ is 6 units.
• The side adjacent angle θ is 5 units.
• The hypotenuse is √(61) units.

`\boxed{\begin{minipage}{8cm}\underline{Trigonometric ratios}\\\\$\sf \sin(\theta)=(O)/(H)\quad\cos(\theta)=(A)/(H)\quad\tan(\theta)=(O)/(A)$\\\\\\$\sf\csc(\theta)=(H)/(O)\quad\sec(\theta)=(H)/(A)\quad\cot(\theta)=(A)/(O)$\\\\where:\\\phantom{ww}$\bullet$ $\theta$ is the angle.\\\phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle.\\\phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle.\\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse.\\\end{minipage}}`

Substitute the given values into each ratio:

`\csc \theta=(√(61))/(6)`

`\sin \theta=(6)/(√(61))`

`\cot \theta=(5)/(6)`

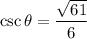
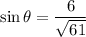
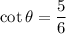
Note: The sin θ ratio can also be written as:

`\implies \sin \theta=(6)/(√(61))\cdot (√(61))/(√(61))`

`\implies \sin \theta=(6√(61))/(61)`