Question

The wet density of a gravel was found to be 2.32 Mg/m^3 and the field water content was 16%. In the laboratory, the density of the solids was found to be 2.70 Mg/m^3, and the maximum and minimum void ratios were 0.59 and 0.28, respectively. Calculate the relative density (Dr) of the gravel in the field.

Answer 1

the relative density of the gravel in the field is 0.7365 or 73.65%

Step-by-step explanation:

Given that;

wet density of gravel
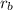`r_(b)` = 2.3 Mg/m³

field water content w = 16%

density of solids in lab
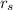`r_(s)` = 2.70 Mg/m³

Maximum void ratio
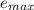`e_(max)` = 0.59

Minimum void ratio
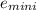`e_(mini)` = 0.28

first we determine the dry density of gravel
`r_(d)` =
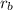`r_(b)` / 1+ w

`r_(d)` = 2.3 Mg/m³ / 1 + 0.16 = 2.3/1.16 = 1.9827 Mg/m³

we know that;
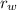`r_(w)` = 1000 kg/m³ = 1 g/cm³

Specific Gravity of soil G =
`r_(s)` /
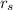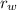`r_(w)` = 2.70 Mg/m³ / 1 = 2.70 Mg/m³

eo = ((G×
`r_(w)`)/
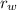`r_(d)`) - 1

eo = (( 2.70 × 1) / 1.9827 ) - 1

eo = 1.3617 - 1

Co = 0.3617

so Relative density
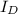`I_(D)` will be;

`I_(D)` =
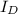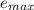`e_(max)` - eo /
`e_(max)` -
`e_(mini)`

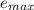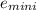
we substitute

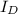`I_(D)` = 0.59 - 0.3617 / 0.59 - 0.28

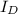`I_(D)` = 0.2283 / 0.31

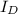`I_(D)` = 0.7365 or 73.65%

Therefore; the relative density of the gravel in the field is 0.7365 or 73.65%