Question

Use synthetic division to determine if x +3 is a factor of the given polynomial


`2x^3+7x^2+3`

Answer 1

After performing synthetic division, as the last number in the bottom row is not zero, this indicates that (x + 3) is not a factor of the given polynomial.

Explanation:

Given polynomial function:

`2x^3+7x^2+3`

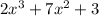
To determine is (x + 3) is a factor of the given polynomial by the method of synthetic division:

• Place "-3" in the division box.
• Write the coefficients of the dividend in descending order.

Note: As the x term is missing, place a zero in its place.

`\begin{array}cccc-3 &2&7&0&3\\\cline{1-1}\end{array}`

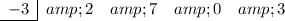
Bring the leading coefficient straight down:

`\begin{array}c-3 &2&7&0&3\\\cline{1-1}&\downarrow&&&\\\cline{2-5}&2&&&\end{array}`

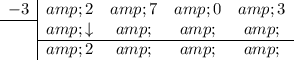
Multiply the number you brought down with the number in the division box and put the result in the next column (under the 7):

`\begin{array}crrr-3 &2&7&0&3\\\cline{1-1}&\downarrow&-6&&\\\cline{2-5}&2&&&\end{array}`

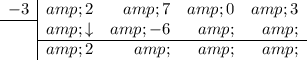
Add the two numbers together and put the result in the bottom row:

`\begin{array}c-3 &2&7&0&3\\\cline{1-1}&\downarrow&-6&&\\\cline{2-5}&2&1&&\end{array}`

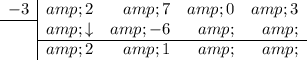
Repeat:

`\begin{array}c-3 &2&7&0&3\\\cline{1-1}&\downarrow&-6&-3&9\\\cline{2-5}&2&1&-3&12\end{array}`

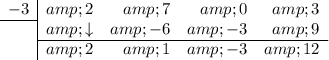
The bottom row (except the last number) gives the coefficients of the quotient. The degree of the quotient is one less than that of the dividend. The last number in the bottom row is the remainder.

Therefore, if we divide the polynomial by (x + 3) we get:

`2x^2+x-3+(12)/(x+3)`

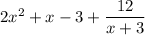
As the last number in the bottom row is not zero, this indicates that (x + 3) is not a factor of the given polynomial.