Answer:
x = 2
Explanation:
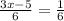
In order to solve this, you must get the denominator off of the left-hand side of the equation, by multiplying 6 on each side, in order to get the denominators to cancel. This leaves you with:
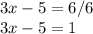
Then, you add 5 to each side.
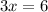
Divide by 3, to get x by itself.
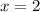
Which gets us to our final answer of x = 2.
Then, you can plug x back into the equation just to double-check yourself:

I hope that this helped you understand to concept a little better. Good luck.