Question

There is three consecutive even integers such that three times the second is six more than the sum of the first and third. Find the three integers.

Answer 1

Let x be the first even integer. So the other two numbers can be obtained as

x+2 and x+4, where x+2 is the second even integer and x+4 is the third even integer.

Now, we want to translate the given property into an equation. We are told "three times the second", so this translates to the expression

`3\cdot(x+2)`

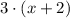
now, we are told that this is six more than the sum of the first and the third. That is, we sum the first and the third and then add 6. This would give us this quantity. So we have

`x+(x+4)+6=3\cdot(x+2)`

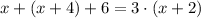
if we expand the factors on the right, we get

`x+(x+4)+6=3x+6`

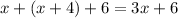
now, we can subtract 6 on both sides, so we get

`x+(x+4)=3x`

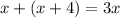
If we operate on the left, we get

`2x+4=3x`

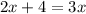
if we subtract 2x on both sides, we get

`4=3x\text{ -2x = x}`

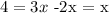
so we have that the first integer is 4. THis means that the other two integers are 6 and 8.