Question

Geometry: Find VT

filler filler filler filler filler filler filler filler filler filler filler filler filler filler
filler

Answer 1

VT = 5.4

Explanation:

Δ SRT and Δ VUT are similar , by the AA postulate.

Then the ratios of corresponding sides are in proportion, that is

`(ST)/(VT)` =
`(SR)/(VU)` ( substitute values )

`(3x-3+x+2)/(x+2)` =
`(14)/(6)`

`(4x-1)/(x+2)` =
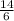
`(7)/(3)` ( cross- multiply )

3(4x - 1) = 7(x + 2) ← distribute parenthesis on both sides

12x - 3 = 7x + 14 ( subtract 7x from both sides )

5x - 3 = 14 ( add 3 to both sides )

5x = 17 ( divide both sides by 5 )

x =
`(17)/(5)` = 3.4

Then

VT = x + 2 = 3.4 + 2 = 5.4