Question

A basketball coach kept stats for his team in free throw percentage and steals (among others). At the last game, Erin's free throw percentage was 79% and she had 4 steals. The team averaged 87% from the free throw line with a standard deviation of 12 and they averaged 7 steals with a standard deviation of 3. In which category did Erin do better compared with her team

Answer 1

Due to the higher z-score, she did better in the free throw category.

Explanation:

Z-score:

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

In this question:

She did better in the category that she had the higher z-score:

Free-throws:

Her free throw percentage was 79%, which means that
`X = 79`

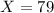
The team averaged 87% from the free throw line with a standard deviation of 12, which means that
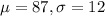`\mu = 87, \sigma = 12`. So

`Z = (X - \mu)/(\sigma)`

`Z = (79 - 87)/(12)`

`Z = -0.67`

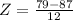
Steals:

She had 4 steals, which means that
`X = 4`

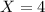
Averaged 7 steals with a standard deviation of 3, which means that
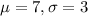`\mu = 7, \sigma = 3`. So

`Z = (X - \mu)/(\sigma)`

`Z = (4 - 7)/(3)`

`Z = -1`

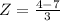
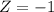
Due to the higher z-score, she did better in the free throw category.