Question

If the car has a mass of 0.2 kg, the ratio of height to width of the ramp is 12/75, the initial displacement is 2.25 m, and the change in momentum is 0.58 kg*m/s, how far will it coast back up the ramp before changing directions

Answer 1

l = 0.548 m

Step-by-step explanation:

For this exercise we compensate by finding the speed of the car

p = m v

v = p / m

v = 0.58 / 0.2

v = 2.9 m / s

this is how fast you get to the ramp, let's use conservation of energy

starting point. Lowest point

Em₀ = K = ½ m v²

final point. Point where it stops on the ramp

`Em_(f)` = U = m g h

mechanical energy is conserved

Em₀ = Em_{f}

½ m v² = m g h

h =
`(m v^2)/(2 g)`

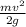
let's calculate

h =
`(0.2 \ 2.9^2)/(2 \ 9.8)`

h = 0.0858 m

to find the distance that e travels on the ramp let's use trigonometry, we look for the angle

tan θ = y / x

tan θ = 12/75 = 0.16

θ = tan⁻¹ 0.16

θ = 9º

therefore

sin 9 = h / l

l = h / sin 9

l = 0.0858 / sin 9

l = 0.548 m