Question

Find the indicated probability.

An archer is able to hit the bull's-eye 53% of the time. If the archer shoots 10 arrows, what is the probability they get exactly 4 bull's-eyes? Assume each shot is independent of the others.
0.0789
0.0905
0.179
0.821

Answer 1

C) 0.179

Explanation:

Since the trials are independent, this is a binomial distribution:

Recall:

• Binomial Distribution -->
  `P(k)={n\choose k}p^kq^(n-k)`
• 
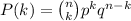
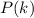  `P(k)` denotes the probability of
  `k` successes in
  `n` independent trials
• 
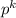  `p^k` denotes the probability of success on each of
  `k` trials
• 
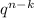  `q^(n-k)` denotes the probability of failure on the remaining
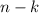  `n-k` trials
• 
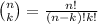  `{n\choose k}=(n!)/((n-k)!k!)` denotes all possible ways to choose
  `k` things out of
  `n` things

Given:

• 
  `n=10`
• 
  `k=4`
• 
  `p^k=0.53^4`
• 
  `q^(n-k)=(1-0.53)^(10-4)=0.47^6`
• 
  `{n\choose k}={10\choose 4}=(10!)/((10-4)!4!)=210`

Calculate:

• 
  `P(4)=(210)(0.53^4)(0.47^6)=0.1786117069\approx0.179`

Therefore, the probability that the archer will get exactly 4 bull's-eyes with 10 arrows in any order is 0.179