Question

Determine the constants a and b so that the function f(x)=ax^3 + bx has a local maximum at the point: (1,6)

Answer 1

The function given is:

`f(x)=ax^3+bx`

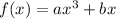
And has a local maximum at (1, 6). Since it has a local extrema in x = 1, this means that the derivative of f(x) at x = 1 is 0:

`Maximum:f^(\prime)(1)=0`

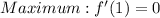
Since we know that the point (1, 6) lies in the graph of the function, we can write:

`\begin{gathered} 6=a\cdot1^3+b\cdot1 \\ . \\ 6=a+b \end{gathered}`

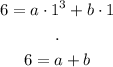
We have an equation that relates a and b, we need to find another one. Let's differentiate f(x):

`(d)/(dx)f(x)=(d)/(dx)(ax^3+bx)=(d)/(dx)(ax^3)+(d)/(dx)(bx)=a\cdot(d)/(dx)(x^3)+b\cdot(d)/(dx)x=a\cdot3x^(3-1)+b\cdot1x^(1-1)=3ax^2+b`

Thus:

`f^(\prime)(x)=3ax^2+b`

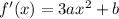
We know that f'(1) = 0, thus:

`\begin{gathered} 0=3a\cdot1^2+b \\ . \\ 0=3a+b \end{gathered}`

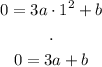
Now, we have a system of two linear equations:

`\begin{cases}6={a+b} \\ 0={3a+b}\end{cases}`

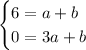
We can subtract the second equation to the first one, to solve by elimination:

`6-0=a+b-(3a+b)`

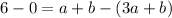
And solve:

`\begin{gathered} 6=a-3a+b-b \\ . \\ 6=-2a \\ . \\ a=(6)/(-2)=-3 \end{gathered}`

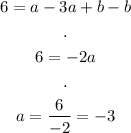
We have found the value of a = -3. Now, we can find b, using the first equation:

`\begin{gathered} 6=-3+b \\ . \\ b=6+3=9 \end{gathered}`

Thus, the answer is:

a = -3

b = 9

We can also check if the result we get is correct:

`\begin{cases}a={-3} \\ b={9}\end{cases}\Rightarrow\begin{cases}f(x)={-3x^3}+9x \\ f^(\prime)(x)={-9x^2+9}\end{cases}`

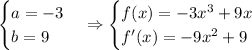
And we should get f(1) = 6 and f'(1) = 0:

`\begin{gathered} f(1)=-3\cdot1^3+9\cdot1=-3+9=6 \\ f^(\prime)(1)=-9\cdot1+9=-9+9=0 \end{gathered}`

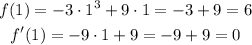
The values we got are correct.