Question

Which two equations would be most appropriately solved by using the quadratic formula?

Select each correct answer.



Responses


A) 3x² = 9

B) −(x−3)(x+9)=0

C) −2x^2+5x=7

D) 0.25x^2+0.8x-8=0




Solve for x.

4x^2+6=40

Round to the nearest hundredth

The solutions are approximately _ and _.

Answer 1

For the first one:

C) −2x^2+5x=7

D) 0.25x^2+0.8x-8=0

For the second one:

`x=\sqrt{(17)/(2)},\:x=-\sqrt{(17)/(2)}`

`x=2.92 \text { and } x=-2.92\;\;\;\;\ \text{ (rounded to 2 decimal places)}`

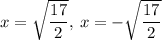
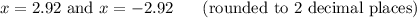
Explanation:

First question:
Choices A and B are easily solved without resorting to quadratic formula

(A) 3x² = 9 ==> x² = 3 ==> x = ± √3

(B) -(x -3)(x-9) ==> x - 3 = 0 or x + 9 = 0 giving x = 3 or x = -9

The other two require the quadratic formula

Second question

`4x^2+6=40\\\\\mathrm{Move}\:6\:\mathrm{to\:the\:right\:side}\\4x^2=34\\\\\mathrm{Divide\:both\:sides\:by\:}4\\(4x^2)/(4)=(34)/(4)\\\\\mathrm{Simplify}\\x^2=(17)/(2)\\\\\\x = \pm \sqrt{(17)/(2)}\\\\\text{The solutions are $x = \sqrt{(17)/(2)}$ and $x = -\sqrt{(17)/(2)}$}`

I cannot see the answer choices; if you want them in decimals then they are:
x=2.91547 and x=-2.91547