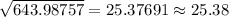Answer:
![12√(2)\sqrt[4]{5}](https://img.qammunity.org/2024/formulas/mathematics/high-school/8kbuebzwvtk8l832v0kdxidu9ko5nu84rt.png)
or
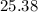
Explanation:
We are given:
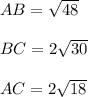
Simplify each square root to the lowest radical:
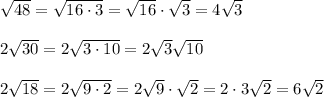
Multiplying all three:
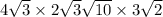
First multiply all terms not under square root:
4 x 2 x 6 = 48
Then multiply all the radicals which are the same:
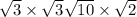
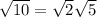
This works out to
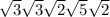
Rearranging the radicals
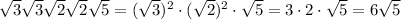
Multiplying by 48, the value we got by multiplication of the terms not under square root we get this value as:
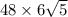
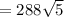
= 643.98757
This is equal to
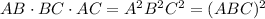
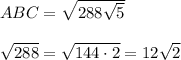
![\sqrt{√(5)} = \sqrt[4]{5}](https://img.qammunity.org/2024/formulas/mathematics/high-school/u6qhbbixs76nhkuzingbpsdfo3p21jkmsk.png)
ABC =
![12√(2)\sqrt[4]{5}](https://img.qammunity.org/2024/formulas/mathematics/high-school/8kbuebzwvtk8l832v0kdxidu9ko5nu84rt.png)
In decimal this would be