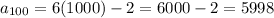Question

the second and sixth term of an A.P are 10 and 34 .find the common difference,first term,nth term and 1000th term​

Answer 1

• Common difference = 6
  
• First term = 4
  
• nth term: aₙ = 6n - 2
  
• 1000th term = 5998

Explanation:

The general equation for the nth term of an AP is:

`a_n = a_1 + d(n-1)\\\\where\\\\a_1 \text{= first term}\\d = \text{common difference}\\\\\text{We are given the second term $a_2$ and the sixth term, $a_6$}\\`

Using the generalized formula

`\begin {aligned}a_2 & = a_1 + d(2 - 1)\\& = a_1 + d\\\end{aligned}\\`

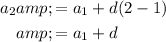
We are also given the second term a₂ = 10
So,

`a_1 + d = 10 \cdots\cdots(1)`'

Sixth term is

`\begin{aligned}a_6 & = a_1 + d(6 - 1)\\& = a_1 + 5d \\\end{alogned}`

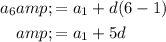
Since 6th term is 34 we get:

`a_1 + 5d = 34 \cdots\cdots(2)`

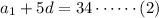
Subtract (1) from (2) to get

`a_1 + 5d - a_1 + d = 34 - 10\\\\4d = 24\\\\d = 6\\\\`

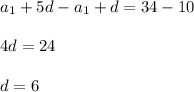
Common difference = 6

Substituting d = 6 in equation (1):

`a_1 + 6 = 10\\a_1 = 10 - 6 = 4\\`

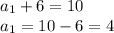
First term is 4

nth term is therefore:

`\\\begin{aligned}a_n &= 4 + 6(n-1)\\& = 4 +6n - 6\\&= 6n - 2\\\end{aligned}`

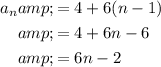
100th term:

`a_(100) = 6(1000) - 2 = 6000 - 2 = 5998`