Question

PLEASE HELP!! Triangle IJK is similar to triangle LMN. Find the measure of side NL. Round your answer to the nearest tenth if necessary. Figures are not drawn to scale.

​

Answer 1

The measure of side NL is 10.1 to the nearest tenth.

Explanation:

In similar triangles, corresponding sides are always in the same ratio.

Therefore, if triangle IJK is similar to triangle LMN:

`\implies \sf IJ:LM=JK:MN=KI:NL`

From inspection of the given triangles:

• JK = 52
• KI = 25
• MN = 21

To find the measure of side NL, substitute the given values into the ratio:

`\implies \sf JK:MN=KI:NL`

`\implies \sf 52:21=25:NL`

`\implies \sf (52)/(21)=(25)/(NL)`

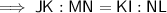
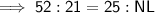
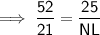
Solve the ratio for NL:

`\implies \sf NL \cdot 52=25 \cdot 21`

`\implies \sf NL=(25 \cdot 21)/(52)`

`\implies \sf NL=10.0961538...`

`\implies \sf NL=10.1\;(nearest\;tenth)`

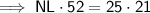
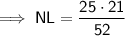
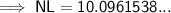
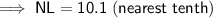
Therefore, the measure of side NL is 10.1 to the nearest tenth.

Answer 2

NL ≈ 10.1

Explanation:

given the triangles are similar then the ratios of corresponding sides are in proportion , that is

`(NL)/(KI)` =
`(MN)/(JK)` ( substitute values )

`(NL)/(25)` =
`(21)/(52)` ( cross- multiply )

52 NL = 25 × 21 = 525 ( divide both sides by 52 )

NL =
`(525)/(52)` ≈ 10.1 ( to the nearest tenth )