Question

Solve the right triangle.
W
√57
U
2√19
V

Answer 1

Explanation:

By Partago theory

The Sum of two right angle triangle must equal to it hypothes

Answer 2

UV = √19

∠V= 60°

∠W = 30°

Explanation:

By Pythagoras Theorem,
`A^(2)+B^(2)=C^(2)`, where C is the hypotenuse, and A and B are the two smaller sides.

Therefore,
`UV^(2) =(2√(19))^(2)- (√(57) )^(2)`

`UV^(2)=76-57=19\\UV=√(19)`

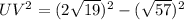
To find the measures of ∠V and ∠W, using right angle trigonometry (SOH CAH TOA). You can actually use any trig ratio, sine (opposite/hypotenuse), cosine (adjacent/hypotenuse), or tangent (opposite/adjacent) to find your designated angle, but I'll just use an appropriate one.

Tan∠V = opposite/adjacent = WU/UV =
`\frac{√(57) }{\sqrt[]{19} }`

∴∠V=
`tan^(-1) (\frac{√(57) }{\sqrt[]{19} })`

∴∠V= 60°

Finally, you could use trigonometry again to find the other unknown angle, or you could use logic, using the property that the angle sum of a triangle = 180°, and the fact that you already have 2 angles.

∴∠W = 180° - 60° - 90°

∠W = 30°