Question

Find the amount in a continuously compounded account for the following condition.

<
Principal, $4000, Annual interest rate, 5.5%; time, 5 years
The balance after 5 years is $

Answer 1

To find the amount in a continuously compounded account, we can use the formula A = Pe^rt, where A is the final amount, P is the principal, r is the annual interest rate, and t is the time in years.

Plugging in the given values, we get:

A = 4000e^(0.055 * 5)

A = 4000e^0.275

A = 5466.76

Therefore, the balance after 5 years is $5466.76.

Explanation:

Answer 2

The balance of the account is $5,266.12.

Explanation:

To calculate the amount in a continuously compounded account, use the continuous compounding interest formula.

`\boxed{\begin{minipage}{8.5 cm}\underline{Continuous Compounding Interest Formula}\\\\$ A=Pe^(rt)$\\\\where:\\\\ \phantom{ww}$\bullet$ $A =$ final amount \\\phantom{ww}$\bullet$ $P =$ principal amount \\\phantom{ww}$\bullet$ $e =$ Euler's number (constant) \\\phantom{ww}$\bullet$ $r =$ annual interest rate (in decimal form) \\\phantom{ww}$\bullet$ $t =$ time (in years) \\\end{minipage}}`

Given values:

• P = $4,000
• r = 5.5% = 0.055
• t = 5 years

To calculate the balance of the investment after 5 years, substitute the given values into the continuous compounding interest formula:

`\implies A=4000e^((0.055 * 5))`

`\implies A=4000e^(0.275)`

`\implies A=4000(1.31653067...)`

`\implies A=5266.12269...`

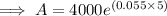
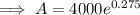
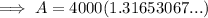
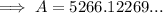
Therefore, the balance of the account after 5 years is $5,266.12.