Question

What is the mADC? Show all work. Rhombus ABCD has a diagonal BD, mADB = (5x-13.3)°, and mCDB = (3x+7.3)°.

Answer 1

76.4°

Explanation:

for figure see attachment.

from the figure,

mADC = mADB + mBDC

from the question,

mADB = (5x - 13.3)°

mCDB = (3x + 7.3)°

hence ,

mADC = (5x -13.3 + 3x + 7.3)°

mADC = (8x - 6)°

again , we know that the diagonals of a rhombus bisect each other . So the given two unknown angles are equal to each other. So that ;

5x - 13.3 = 3x +7.3

5x - 3x = 7.3+ 13.3

2x = 20.6

x = 20.6/2

x = 10.3

plug in this value of x in the measure of angle ADC as,

angADC = 8*10.3 -

angADC = 82 .4 - 6

angADC = 76.4°

and we are done!

Answer 2

m∠ADC = 76.4°

Explanation:

Properties of a Rhombus:

• All sides are equal in length.
• Diagonals bisect each other at 90°.
• Opposite angles are equal.
• Opposite sides are parallel.
• Adjacent angles sum to 180°.

Each diagonal of a rhombus bisects the angle through which it passes.

Therefore, if rhombus ABCD has a diagonal BD, then BD bisects angle B and angle D. This means that ∠ADB equals ∠CDB.

Therefore, to find the value of x, equate ∠ADB and ∠CDB:

`\implies \angle ADB= \angle CDB`

`\implies (5x-13.3)^(\circ)=(3x+7.3)^(\circ)`

`\implies 5x-13.3=3x+7.3`

`\implies 2x=20.6`

`\implies x=10.3`

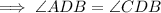
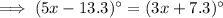
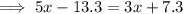
Therefore, the measure of angles ADB and CDB are:

`\implies \angle ADB= (5 \cdot 10.3-13.3)^(\circ)`

`\implies \angle ADB= (51.5-13.3)^(\circ)`

`\implies \angle ADB=38.2^(\circ)`

`\implies \angle CDB=38.2^(\circ)`

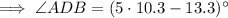
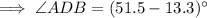
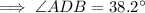
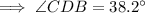
The measure of angle ADC is the sum of angles ADB and CDB:

`\implies \angle ADC= \angle ADB + \angle CDB`

`\implies \angle ADC=38.2^(\circ)+38.2^(\circ)`

`\implies \angle ADC=76.4^(\circ)`

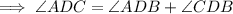
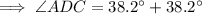
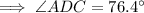
Therefore, the measure of angle ADC is 76.4°.