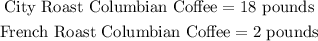let us begin by assigning letters to the variables here. Hence, let the City Roast Colombian be x, while the French Roast Columbian be y. If the mixture of 1 pound of City roast and 1 pound of French roast would cost $7.83 per pound (for the mixture), then we can have the expression developed into an equation as follows;
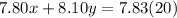
Also, to make a 20 pound blend would simply mean;
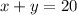
We now have a system of equations which we can solve as follows;
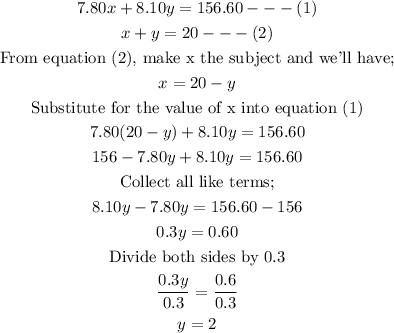
We can now substitute for the value of y into equation (2), as follows;
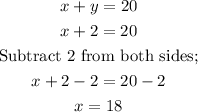
Hence, we have;
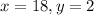
ANSWER:
Julia and her husband should buy the coffee as follows;