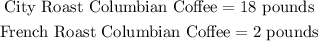Question

Julia and her husband own a coffee shop. They experimented with mixing a City Roast Columbian coffee that cost $7.80 per pound with French Roast Columbian coffee that cost $8.10 per pound to make a 20 pound blend. Their blend should cost them $7.83 per pound. How many pounds of each type of coffee should they buy?

Answer 1

let us begin by assigning letters to the variables here. Hence, let the City Roast Colombian be x, while the French Roast Columbian be y. If the mixture of 1 pound of City roast and 1 pound of French roast would cost $7.83 per pound (for the mixture), then we can have the expression developed into an equation as follows;

`7.80x+8.10y=7.83(20)`

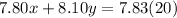
Also, to make a 20 pound blend would simply mean;

`x+y=20`

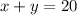
We now have a system of equations which we can solve as follows;

`\begin{gathered} 7.80x+8.10y=156.60---(1) \\ x+y=20---(2) \\ \text{From equation (2), make x the subject and we'll have;} \\ x=20-y \\ \text{Substitute for the value of x into equation (1)} \\ 7.80(20-y)+8.10y=156.60 \\ 156-7.80y+8.10y=156.60 \\ \text{Collect all like terms;} \\ 8.10y-7.80y=156.60-156 \\ 0.3y=0.60 \\ \text{Divide both sides by 0.3} \\ (0.3y)/(0.3)=(0.6)/(0.3) \\ y=2 \end{gathered}`

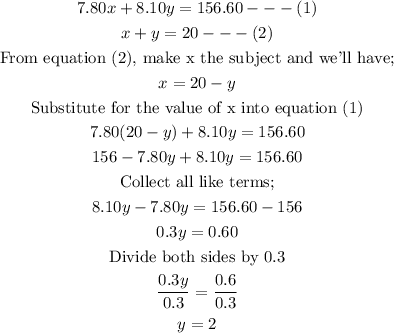
We can now substitute for the value of y into equation (2), as follows;

`\begin{gathered} x+y=20 \\ x+2=20 \\ \text{Subtract 2 from both sides;} \\ x+2-2=20-2 \\ x=18 \end{gathered}`

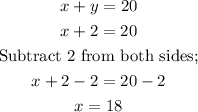
Hence, we have;

`x=18,y=2`

ANSWER:

Julia and her husband should buy the coffee as follows;

`\begin{gathered} \text{City Roast Columbian Coffee}=18\text{ pounds} \\ \text{French Roast Columbian Coffee}=2\text{ pounds} \end{gathered}`